Um Estudo sobre Detecção de Fraude em Cartões de Crédito
As fraudes em cartões de crédito afetam consumidores e instituições financeiras globalmente, representando um
problema significativo. Trata-se de atividades fraudulentas em que criminosos obtêm informações pessoais e
financeiras dos titulares dos cartões para realizar transações não autorizadas. Essas transações fraudulentas
podem envolver desde compras online até saques em dinheiro ou transferências bancárias.
Neste projeto, iremos analisar uma base de dados que contém registros de transações realizadas com cartões de
crédito, incluindo transações normais e fraudulentas.
Após a análise da base de dados, iremos criar um modelo de machine learning com a finalidade de
classificar se
uma determinada transação foi considerada normal ou uma fraude.
# Bibliotecas para tratarmos e visualizarmos os dados
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
# Bibliotecas com os modelos de machine learning
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
# Bibliotecas para separar os dados
from sklearn.model_selection import train_test_split
from imblearn.under_sampling import RandomUnderSampler
# Bibliotecas para a avaliação dos modelos
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.metrics import confusion_matrix
set.sns()
Importando os dados
O conjunto de dados disponibilizado refere-se a transações efetuadas por titulares de cartões de crédito
europeus no mês de setembro de 2013. Este conjunto contém apenas variáveis numéricas de entrada que foram
obtidas por meio de uma transformação PCA. Devido a preocupações com a confidencialidade, não foram fornecidos
os nomes originais das colunas, sendo assim, elas são identificadas como [V1, V2, V3 ... V28].
Além disso, é importante mencionar a existência da coluna "Time". Os dados foram coletados ao longo de um
período de dois dias, e a coluna "Time" indica o exato segundo em que cada transação ocorreu dentro desse
intervalo. No entanto, iremos utilizar essa coluna apenas para visualização dos dados. Para facilitar essa
visualização, criei uma outra coluna chamada "Hour", que registra apenas a hora da transação, sem considerar
os segundos.
Outras colunas presentes no conjunto de dados incluem:
- Hour: Indica a hora em que a transação foi realizada dentro do intervalo de dois dias (0-48 horas).
- Amount: Representa o valor gasto na transação.
- Class: Essa coluna possui valores binários (0, 1).
- 0: Indica que a transação é considerada normal.
- 1: Indica que a transação é classificada como fraudulenta.
data = pd.read_csv('database/creditcardfraud.csv')
data['Hour'] = data['Time'] // 3600
df = data.drop('Time', axis=1)
Visualizando as 5 primeiras linhas
| V1 | V2 | V3 | ... | V28 | Amount | Class | Hour | |
|---|---|---|---|---|---|---|---|---|
| 0 | -1.359807 | -0.072781 | 2.536347 | ... | -0.021053 | 149.62 | 0 | 0.0 |
| 1 | 1.191857 | 0.266151 | 0.166480 | ... | 0.014724 | 2.69 | 0 | 0.0 |
| 2 | -1.358354 | -1.340163 | 1.773209 | ... | -0.059752 | 378.66 | 0 | 0.0 |
| 3 | -0.966272 | -0.185226 | 1.792993 | ... | 0.061458 | 123.50 | 0 | 0.0 |
| 4 | -1.158233 | 0.877737 | 1.548718 | ... | 0.215153 | 69.99 | 0 | 0.0 |
Analisando a base de dados
A base de dados contém 284807 linhas e 31 colunas.
Nas quais 284315 representam as transações normais, e 492 representam as transações fraudulentas.
Quando comparamos com o total de registros, as fraudes representam MENOS de 1% dos casos, mais precisamente
0.173% dos casos
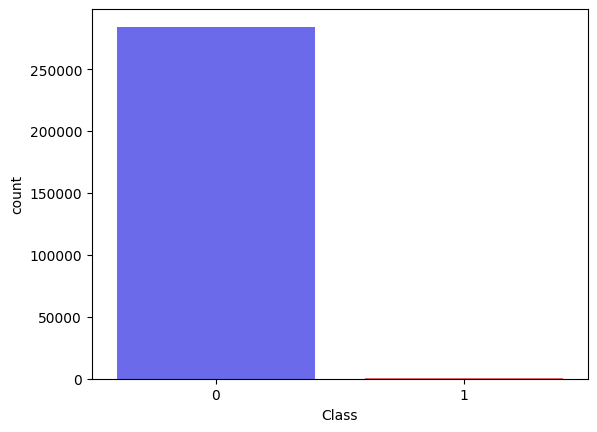
Transações normais x Transações Fraudulentas
A quantidade de Class 0(Transação normal) com a quantidade de Class 1 (Transação fraudulenta) na base de dados.
Analisando alguns dados estatísticos sobre nossa base de dados, no caso Hour, Amount e Class.
Podemos ver algo interessante na coluna Amount, A média de gastos é 88,34, porém a mediana é de 22,00. Isso
mostra que há um valor discrepante dos outros que está elevando o valor da média a tornando distante do valor
da mediana. E quando olhamos para o MAX da coluna amount podemos ver que o valor maximo foi de 25.691,16
| Hour | Amount | Class | |
|---|---|---|---|
| count | 284807.00 | 284807.00 | 284807.00 |
| mean | 25.84 | 88.34 | 0.01 |
| std | 13.18 | 250.12 | 0.04 |
| min | 0.00 | 0.00 | 0.00 |
| 25% | 15.00 | 5.60 | 0.00 |
| 50% | 23.00 | 22.00 | 0.00 |
| 75% | 38.00 | 77.16 | 0.00 |
| max | 47.00 | 25691.16 | 1.00 |
Visualizando alguns dados
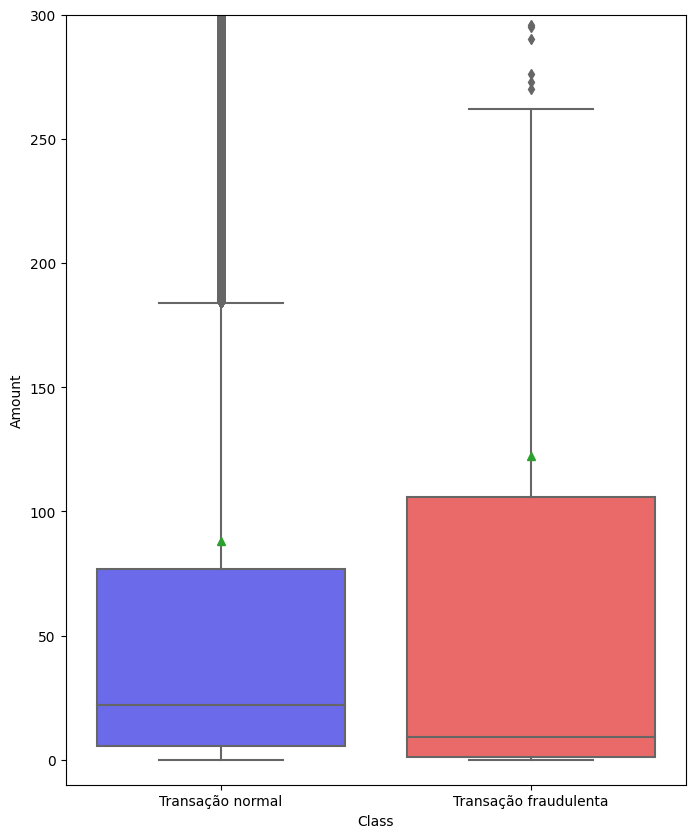
Usando boxplot, podemos analisar a quantia gasta em uma transação normal e a quantia gasta nas transações
fraudulentas.
Nas transações normais podemos ver que:
- A mediana(risco dentro da primeira caixa) é um valor abaixo dos 50, provavelmente próximo de 20;
- E a média nas transações normais(pequeno triangulo acima da caixa) é um valor abaixo dos 100, próximo de 90.
- A mediana é bem mais baixa, diria que inferior a 10;
- Por outro lado a média supera os 100 das transações normais, algo próximo a 120.
- Nas transações normais eles começam pouco abaixo de 200;
- E nas transações fraudulentas acima de 250.
fig, ax = plt.subplots(figsize=(8,10))
#means é o ponto verde que indica o valor da média
sns.boxplot(x=df.Class, y=df.Amount,means=True, ax=ax, palette='seismic')
# Tamanho do eixo Y, inicio, fim
ax.set_ylim(-10, 300)
# Labels dos boxplots
plt.xticks([0, 1], ['Transação normal', 'Transação fraudulenta'])
plt.show()
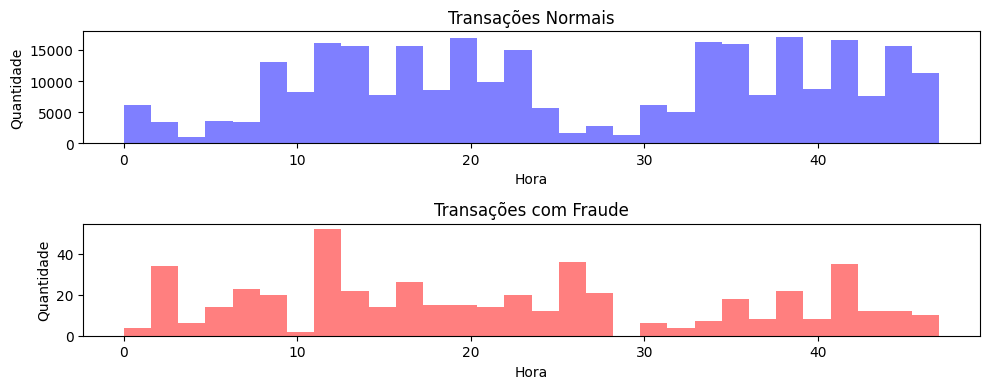
Aqui foram plotados dois histogramas para analisar a frequência das transações com cartões de
crédito.
O primeiro histograma exibe as transações normais e as respectivas horas em que foram realizadas. O segundo
histograma exibe as transações fraudulentas.
O objetivo é identificar se existe algum horário de pico para algum tipo de transação específico. No entanto,
não foi identificado nenhum padrão evidente.
# Separando a base de dados com dados somente fraudulentos, e dados somente normais
normal = df[df['Class'] == 0]
fraude = df[df['Class'] == 1]
# Criando o subplot com duas áreas (1 linha, 2 colunas)
fig, ax = plt.subplots(nrows=2, ncols=1, figsize=(10, 4))
# Plotando o histograma de transações normais
ax[0].hist(normal.Hour, bins=30, color='blue', alpha=0.5)
ax[0].set_title('Transações Normais')
ax[0].set_xlabel('Hora')
ax[0].set_ylabel("Quantidade")
# Plotando o histograma de transações com fraude
ax[1].hist(fraude.Hour, bins=30, color='red', alpha=0.5)
ax[1].set_title('Transações com Fraude')
ax[1].set_xlabel('Hora')
ax[1].set_ylabel("Quantidade")
plt.tight_layout()
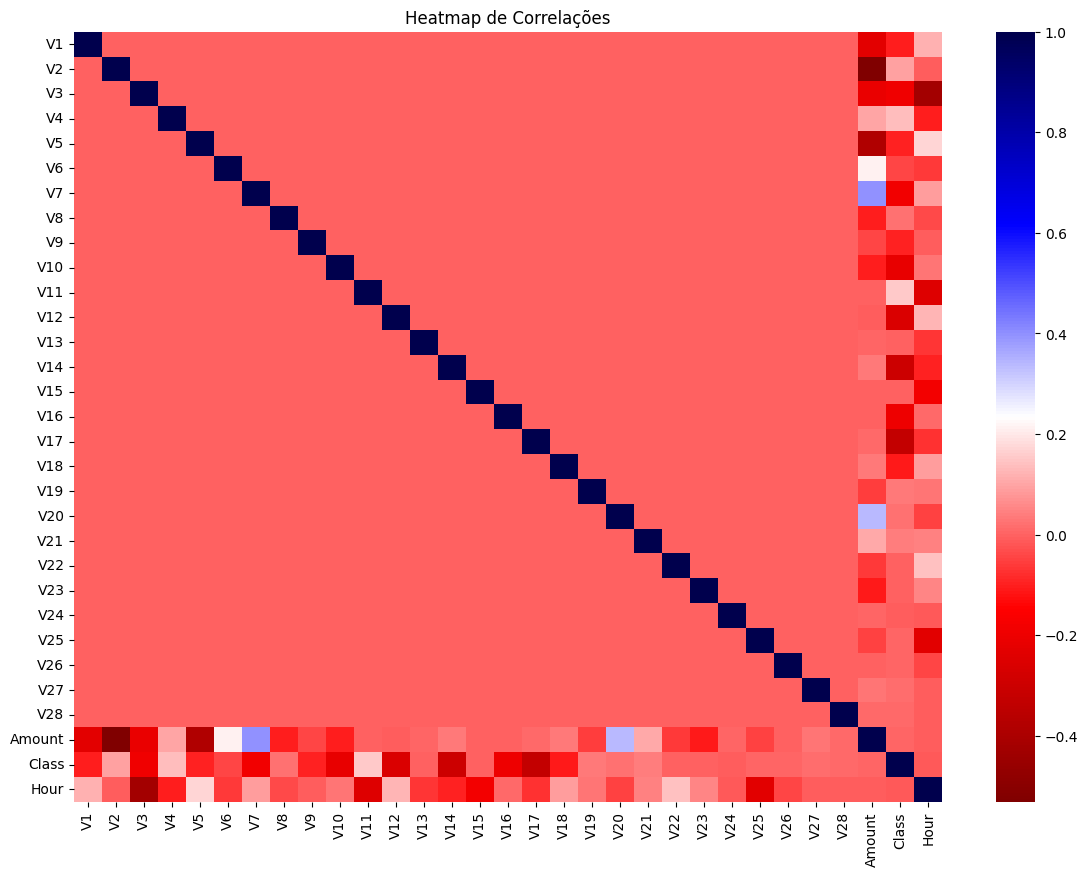
A seguir, é exibido um heatmap (mapa de calor) que representa as correlações entre as variáveis.
Essas
correlações indicam o quanto uma variável influencia a outra.
Neste contexto, em que estamos analisando
transações fraudulentas, é importante destacar a coluna 'Class'. Quanto menos clara a cor da célula, maior é a
influência dessa variável no valor da coluna 'Class'.
# Calcula a matriz de correlações
correlations = df.corr()
# Cria o heatmap de correlações
plt.figure(figsize=(14, 10))
sns.heatmap(correlations, cmap='seismic_r')
# Configurações adicionais
plt.title('Heatmap de Correlações')
plt.show()
Criação dos modelos supervisionados de classificação
Após alguns testes notei que remover as colunas Amount e Hour ajudariam numa melhor taxa de
acerto.
Separação dos dados
Antes de criarmos os modelos, é importante observar um fato crucial. Nossa base de dados contém mais de
284.000 registros, sendo que menos de 1% deles são fraudes. Portanto, se desenvolvermos um modelo que
classifique todos os registros como normais, tecnicamente ele terá uma taxa de acerto superior a 99%. Embora
essa porcentagem seja excelente, usar esse modelo seria o mesmo que não usar nada.
Para contornar essa situação, usei classe RandomUnderSampler da biblioteca imblearn. Essa classe irá realizar
o seguinte procedimento: selecionar todos os registros da Classe 1 e, aleatoriamente, escolher a mesma
quantidade de registros da Classe 0. Dessa forma, obteremos uma nova base de dados com uma distribuição
equilibrada, contendo 50% de valores normais e 50% de registros fraudulentos.
X = df.drop(["Class", "Amount", "Hour"], axis=1)
y = df.Class
# usar técnica under-sampling
rus = RandomUnderSampler()
X_rus, y_rus = rus.fit_resample(X=X, y=y)
# dividindo o dataset entre treino e teste
X_train, X_test, y_train, y_test = train_test_split(X_rus, y_rus, shuffle=True)
# plotar a nova distribuição de classes
sns.countplot(x=y_rus, palette='seismic');
Quais modelos e por quê?
Decidi criar e avaliar três modelos diferentes para a detecção de fraudes em cartões de crédito. São eles:
- Regressão Logística: É amplamente utilizado na detecção de fraudes de cartões de crédito, especialmente para problemas de classificação binária (0, 1).
- Random Forest: São modelos altamente eficazes para a detecção de fraudes em cartões de crédito. Eles possuem a capacidade de lidar com conjuntos de dados volumosos e capturar características importantes e relacionamentos não lineares.
- SVM (Support Vector Machines): Têm sido amplamente empregadas na detecção de fraudes. Ao utilizar kernels adequados, as SVMs são especialmente úteis para identificar padrões complexos e transações fraudulentas.
np.random.seed(2)
regressao = LogisticRegression(max_iter=1000).fit(X_train, y_train)
florest = RandomForestClassifier(max_samples=6, criterion="entropy").fit(X_train, y_train)
svm = SVC().fit(X_train, y_train)
#Fazendo as previsões em cima dos dados de teste
y_regressao = regressao.predict(X_test)
y_florest = florest.predict(X_test)
y_svm = svm.predict(X_test)
Avaliando os modelos
Após criar e treinar os modelos, realizamos a previsão utilizando os dados de teste.
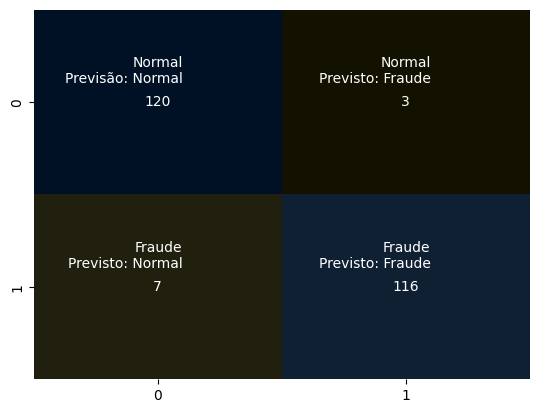
Agora, vamos analisar a matriz de confusão, que nos permite comparar os valores reais com os valores previstos
pelo modelo.
Nosso objetivo é obter a maior precisão possível. Para isso, buscamos ter o maior número de acertos na
diagonal principal, indicando que os valores foram previstos corretamente. Por outro lado, procuramos ter o
menor número possível na diagonal secundária, que indica os valores previstos incorretamente.
A matriz de confusão é uma ferramenta valiosa para avaliar o desempenho dos nossos modelos de previsão. Ela
nos fornece uma visão clara dos acertos e erros, permitindo-nos identificar áreas em que podemos melhorar e
ajustar nossos modelos de detecção de fraudes em cartões de crédito.
fig, ax = plt.subplots()
# cmap personalizado para gerar somente cores escuras em toda a matriz
cmap = sns.diverging_palette(80, 250, s=100, l=5, as_cmap=True)
# Criação do da matriz confusão usando um heatmap
sns.heatmap(confusion_matrix(y_test, y_regressao), annot=True, fmt=".3g", cmap=cmap, cbar=False, ax=ax)
# Adicionando rótulos personalizados
labels = [['Normal\nPrevisão: Normal', 'Normal\nPrevisto: Fraude'], ['Fraude\nPrevisto: Normal', 'Fraude\nPrevisto: Fraude']]
for i in range(len(labels)):
for j in range(len(labels[i])):
text = ax.text(j + 0.6, i + 0.25, labels[i][j], ha='right', va='top', color='white')
plt.show()
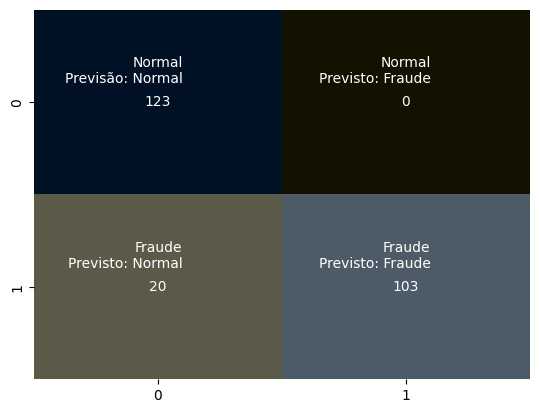
fig, ax = plt.subplots()
sns.heatmap(confusion_matrix(y_test, y_florest), annot=True, fmt=".3g", cmap=cmap, cbar=False, ax=ax)
# Adicionando rótulos personalizados
labels = [['Normal\nPrevisão: Normal', 'Normal\nPrevisto: Fraude'], ['Fraude\nPrevisto: Normal', 'Fraude\nPrevisto: Fraude']]
for i in range(len(labels)):
for j in range(len(labels[i])):
text = ax.text(j + 0.6, i + 0.25, labels[i][j], ha='right', va='top', color='white')
plt.show()
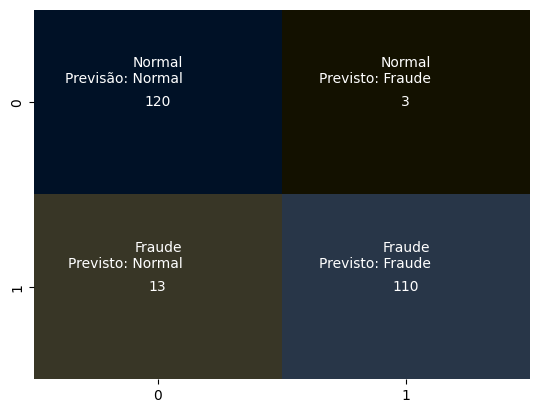
fig, ax = plt.subplots()
sns.heatmap(confusion_matrix(y_test, y_svm), annot=True, fmt=".3g", cmap=cmap, cbar=False, ax=ax)
# Adicionando rótulos personalizados
labels = [['Normal\nPrevisão: Normal', 'Normal\nPrevisto: Fraude'], ['Fraude\nPrevisto: Normal', 'Fraude\nPrevisto: Fraude']]
for i in range(len(labels)):
for j in range(len(labels[i])):
text = ax.text(j + 0.6, i + 0.25, labels[i][j], ha='right', va='top', color='white')
plt.show()
Acurácia, Precisão e Recall
No contexto geral, acurácia, precisão e recall são métricas comumente utilizadas na avaliação de modelos de classificação.
- Acurácia é calculada com os valores da diagonal principal divido pelo total de elementos da matriz de confusão.
- Precisão é uma métrica que mede a taxa de acerto das transações normais. Quanto menos transações NORMAIS classificadas errado, melhor.
- Recall calcula a taxa de acerto das transações fraudulentas. Quanto menos transações FRAUDULENTAS avaliadas errado, melhor.
Importante: Essas métricas são o intervalo de valores entre 0 e 1. Então quanto mais próximo de 1, melhor.
# imprimir a acurácia do modelo, recall e precisao
print("R Logistica: {:.3f}\n".format(accuracy_score(y_test, y_regressao)))
print("R Florest: {:.3f}\n".format(accuracy_score(y_test, y_florest)))
print("SVM: {:.3f}\n".format(accuracy_score(y_test, y_svm)))
R Logistica: 0.959
R Florest: 0.919
SVM: 0.935
# imprimir relatório de classificação
print("R Logistica: {:.3f}\n".format(precision_score(y_test, y_regressao)))
print("R Florest: {:.3f}\n".format(precision_score(y_test, y_florest)))
print("Precisão SVM: {:.3f}\n".format(precision_score(y_test, y_svm)))
R Logistica: 0.975
R Florest: 1.000
SVM: 0.973
# imprimir relatório de classificação
print("R Logistica: {:.3f}\n".format(recall_score(y_test, y_regressao)))
print("R Florest: {:.3f}\n".format(recall_score(y_test, y_florest)))
print("Recall SVM: {:.3f}\n".format(recall_score(y_test, y_svm)))
R Logistica: 0.943
R Florest: 0.837
SVM: 0.894
Conclusão
A detecção de fraudes em cartões de crédito é um desafio complexo, mas por meio do nosso estudo, conseguimos
obter resultados promissores. Em particular, o modelo de regressão logística demonstrou um desempenho
consistente e altamente satisfatório em comparação com os outros dois modelos avaliados.
Este estudo nos permitiu compreender a importância de utilizar métricas como acurácia, precisão e recall para
avaliar o desempenho dos modelos. Identificamos que o recall se mostrou especialmente relevante para garantir
a detecção adequada de transações fraudulentas, minimizando as fraudes mal classificadas.
Através do ajuste contínuo de parâmetros e da exploração de outros modelos, acredito firmemente que podemos
alcançar resultados ainda melhores.